一本通-1367：查找二叉树(tree_a)

【题目描述】 已知一棵二叉树用邻接表结构存储，中序查找二叉树中值为x的结点，并指出是第几个结点。例：如图二叉树的数据文件的数据格式如下:

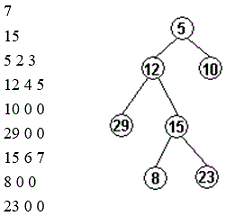
【输入】 第一行n为二叉树的结点个树，n≤100；第二行x表示要查找的结点的值；以下第一列数据是各结点的值，第二列数据是左儿子结点编号，第三列数据是右儿子结点编号。

【输出】 一个数即查找的结点编号。

【输入样例】 7 15 5 2 3 12 4 5 10 0 0 29 0 0 15 6 7 8 0 0 23 0 0

【输出样例】 4

---

最开始的思路是建树，然后辅助栈中序遍历即可，虽然并不需要建树，但是还是练习一下。

#include <bits/stdc++.h>

using namespace std;

struct Node
{
    int val;
    int leftNode, rightNode;
};

struct TreeNode
{
    int val;
    TreeNode *left, *right;
    TreeNode(int x): val(x), left(NULL), right(NULL) {}
};

vector<Node> seq(105);
int n;
int target, step = 0;

TreeNode *build(int pos)
{
    if (!pos) return NULL;

    TreeNode *root = new TreeNode(seq[pos].val);
    root -> left = build(seq[pos].leftNode);
    root -> right = build(seq[pos].rightNode);

    return root;
}

void inorderTraversal(TreeNode *root)
{
    if (!root) return;
    stack<TreeNode*> s;
    TreeNode *p = root;

    while (!s.empty() || p) {
        if (p) {
            s.push(p);
            p = p -> left;
        }
        else {
            p = s.top(); s.pop();
            ++step;
            if (p -> val == target) return;
            p = p -> right;
        }
    }
}

void makeEmpty(TreeNode *& root)
{
    if (root) {
        makeEmpty(root -> left);
        makeEmpty(root -> right);
        delete root;
        root = NULL;
    }
}

int solve()
{
    TreeNode *root = build(1);
    inorderTraversal(root);
    makeEmpty(root);

    return step;
}


int main()
{
    std::ios_base::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);

    cin >> n >> target;
    for (int i = 1; i <= n; ++i) {
        cin >> seq[i].val >> seq[i].leftNode >> seq[i].rightNode;
    }
    cout << solve() << endl;

    return 0;
}

也可以不用建树，因为每个节点已经给出了左右节点的编号，就相当于建树了。

#include <bits/stdc++.h>

using namespace std;

struct Node
{
    int val;
    int leftNode, rightNode;
};

vector<Node> seq(105);
int n;
int target, step = 0;

void inorderTraversal(int pos)
{
    if (seq[pos].leftNode) inorderTraversal(seq[pos].leftNode);

    ++step;
    if (seq[pos].val == target) {
        cout << step << endl;
        exit(0);
    }

    if (seq[pos].rightNode) inorderTraversal(seq[pos].rightNode);
}


int main()
{
    std::ios_base::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);

    cin >> n >> target;
    for (int i = 1; i <= n; ++i) {
        cin >> seq[i].val >> seq[i].leftNode >> seq[i].rightNode;
    }
    inorderTraversal(1);

    return 0;
}