1514.Path with Maximum Probability¶
Tags: Medium Graph
Links: https://leetcode.com/problems/path-with-maximum-probability/
You are given an undirected weighted graph of n nodes (0-indexed), represented by an edge list where edges[i] = [a, b] is an undirected edge connecting the nodes a and b with a probability of success of traversing that edge succProb[i].
Given two nodes start and end, find the path with the maximum probability of success to go from start to end and return its success probability.
If there is no path from start to end, return 0. Your answer will be accepted if it differs from the correct answer by at most 1e-5.
Example 1:
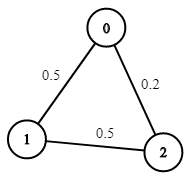
Input: n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.2], start = 0, end = 2
Output: 0.25000
Explanation: There are two paths from start to end, one having a probability of success = 0.2 and the other has 0.5 * 0.5 = 0.25.
Example 2:
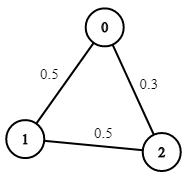
Input: n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.3], start = 0, end = 2
Output: 0.30000
Example 3:
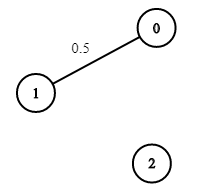
Input: n = 3, edges = [[0,1]], succProb = [0.5], start = 0, end = 2
Output: 0.00000
Explanation: There is no path between 0 and 2.
Constraints:
2 <= n <= 10^40 <= start, end < nstart != end0 <= a, b < na != b0 <= succProb.length == edges.length <= 2*10^40 <= succProb[i] <= 1- There is at most one edge between every two nodes.
从start开始,依次去更新与其相连的点,这些点作为源点再去更新其他点,数组d[i]记录从start到i的最大概率乘积,很典型的BFS套路。
这道题其实是边权重的最大乘积的一种形式,此时边的权重是以概率的形式表示,如果是权重大于1的数,甚至很大,最后结果超过了unsigned long long呢?其实可以将边的权重取log,然后用一个path数组来记录路径,这样就将乘积转化为加法了。当然本题无需这么做也可以求解。
class Solution {
struct Node
{
int to;
double probability;
Node(int t, double p) : to(t), probability(p) {}
};
public:
double maxProbability(int n, vector<vector<int>>& edges, vector<double>& succProb, int start, int end) {
std::ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
vector<vector<Node>> grid(n);
for (int i = 0; i < edges.size(); ++i) {
int from = edges[i][0], to = edges[i][1];
grid[from].push_back(Node(to, succProb[i]));
grid[to].push_back(Node(from, succProb[i]));
}
vector<double> d(n, 0); d[start] = 1;
queue<int> q;
q.push(start);
while (!q.empty()) {
int from = q.front(); q.pop();
for (int i = 0; i < grid[from].size(); ++i) {
int to = grid[from][i].to;
double probability = grid[from][i].probability;
if (d[to] < d[from] * probability) {
q.push(to);
d[to] = d[from] * probability;
}
}
}
return d[end];
}
};