1443.Minimum Time to Collect All Apples in a Tree

Tags: Medium Depth-first Search

Links: https://leetcode.com/problems/minimum-time-to-collect-all-apples-in-a-tree/

---

Given an undirected tree consisting of n vertices numbered from 0 to n-1, which has some apples in their vertices. You spend 1 second to walk over one edge of the tree. Return the minimum time in seconds you have to spend in order to collect all apples in the tree starting at **vertex 0* and coming back to this vertex.*

The edges of the undirected tree are given in the array edges, where edges[i] = [fromi, toi] means that exists an edge connecting the vertices fromi and toi. Additionally, there is a boolean array hasApple, where hasApple[i] = true means that vertex i has an apple, otherwise, it does not have any apple.

Example 1:

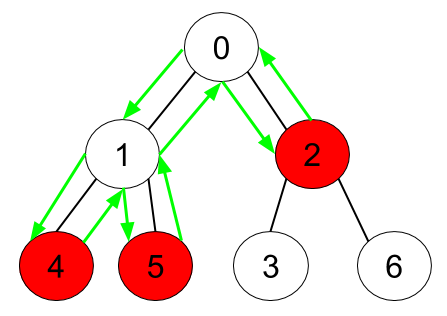
Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,true,false,true,true,false]
Output: 8 
Explanation: The figure above represents the given tree where red vertices have an apple. One optimal path to collect all apples is shown by the green arrows.  

Example 2:

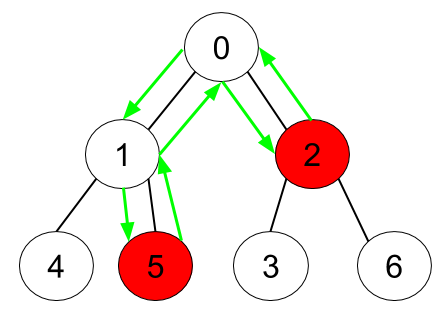
Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,true,false,false,true,false]
Output: 6
Explanation: The figure above represents the given tree where red vertices have an apple. One optimal path to collect all apples is shown by the green arrows.  

Example 3:

Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,false,false,false,false,false]
Output: 0

Constraints:

• 1 <= n <= 10^5
• edges.length == n-1
• edges[i].length == 2
• 0 <= fromi, toi <= n-1
• fromi < toi
• hasApple.length == n

---

用一个哈希表记录从与from节点直接相连的to节点。函数solve用来计算从startPoint开始采摘苹果所需的时间。递归的终止条件是当前节点的出度为0，也就是到了叶节点。

每个节点遍历一次，时间复杂度$O(n)$。

class Solution {
    unordered_map<int, vector<int>> um;
    vector<bool> used;
public:
    int minTime(int n, vector<vector<int>>& edges, vector<bool>& hasApple) {
        std::ios_base::sync_with_stdio(false);
        cin.tie(NULL);
        cout.tie(NULL);

        used.resize(n, false);
        for (auto & e : edges) {
            int from = e[0], to = e[1];
            um[from].push_back(to);
            um[to].push_back(from);
        }

        return DFS(0, hasApple);
    }

    int DFS(int startPoint, vector<bool>& hasApple)
    {
        int res = 0;
        used[startPoint] = true;

        for (auto & e : um[startPoint]) {
            if (!used[e]) {
                int tmp = DFS(e, hasApple);
                if (tmp || (tmp == 0 && hasApple[e])) res += 2 + tmp;
            }
        }

        return res;
    }
};